Yrurtj

この項目では、図形について説明しています。記号文字については「三角 (記号)」をご覧ください。

三角形

三角形（さんかくけい、さんかっけい、拉: triangulum, 独: Dreieck, 英, 仏: triangle, (古風) trigon) は、同一直線上にない3点と、それらを結ぶ3つの線分からなる多角形。その3点を三角形の頂点、3つの線分を三角形の辺という。

記法・定義

点A, 点B, 点C を頂点とする三角形は記号 △ を用いて △ABC と表記する。

三角形の 2 つの辺のなす角をその三角形の内角という。

図 1: 内角と外角

図 1 でいえば、∠ABC が内角の 1 つとなる。三角形は 3 つの内角をもち、その和は平面上では2直角（ 180 度）となる（本稿はユークリッド幾何学における三角形を論じる）。

また、∠ACD のように 1 つの辺と他の辺の延長との間にできる角を三角形の外角という。三角形である頂点（内角）について考えるとき、内角の2辺を除いた残りの辺をその頂点（内角）の対辺という。また、三角形のある辺について考えるとき、辺の両端を除いた残りの頂点（内角）をその辺の対頂点（対角）という。

一般に三角形の頂点やその頂点の内角を表すときには大文字のアルファベットを用いる。特に、内角（内角の大きさ）を表すときには、頂点の前に記号 ∠ をつけるか、頂点の文字を斜体にして表すことがある。たとえば、図 2 の頂点 B を持つ内角（内角の大きさ）を ∠B、または B と表す。また、角の対辺（対辺の長さ）を表すのに、頂点の文字に対応する小文字のアルファベットを用いることが行われる。たとえば、図 2 の角 B の対辺 CA のことを、 b と表すことがある。

三角形を成り立たせる3辺（三角形の成立条件）

三角形のどの辺の長さも他の二辺の長さの和より小さい。すなわち、三角形を構成する3辺の長さを a，b，c とするとき、次の三つの不等式が成り立つ。

a < b+c

b < a+c

c < a+b

この関係は三角不等式として一般化される。
逆に、この不等式が三つとも成り立てば、a，b，c　を3辺の長さとして三角形が作れることが知られている。

三角形の底辺と高さ（中線と中点連結）

三角形の 3 つ辺のうち一つを選んで底辺とし、その対頂点から底辺（またはその延長）に下した垂線から、三角形が切り取る線分（線分の長さ）を、三角形の高さという。どの辺を底辺と見るかによって、三角形には 3 つの高さを考えることができる。
底辺の対頂点を通る、底辺の平行線を引くとき、平行線の間の距離は三角形の高さに等しい。

底辺の中点と、対頂点を結ぶ線分を、三角形の中線という。どの辺を底辺と見るかによって、三角形には 3 つの中線を考えることができる。
三角形の中線は、三角形の面積を二等分する。

底辺を除く 2 つの辺それぞれの中点を結ぶ線分を、三角形の中点連結という。どの辺を底辺と見るかによって、三角形には 3 つの中点連結を考えることができる。
三角形の中点連結は、底辺と平行で、長さは底辺の半分に等しい（三角形の中点連結定理）。

三角形の種類

図 2: 鋭角三角形（不等辺三角形）

三角形はその辺や角によって、いくつかの種類に分けられる。

角の大きさが 0 度より大きく 90 度より小さい場合、その角を鋭角という。

角の大きさが90 度の場合、その角を直角という。

角の大きさが 90 度より大きく 180 度より小さい場合、その角を鈍角という。

三角形の内角の和は 180 度なので、三角形は 90 度以上の大きさの角を 2 つ以上は持てない。三角形の内角は、すべて鋭角であるか、直角を 1 つだけ持ち残りの角は鋭角であるか、鈍角を 1 つだけ持ち残りの角は鋭角であるか、のいずれかである。

図 3: 鈍角三角形

三角形の 3 つの内角の大きさに注目して、すべての角が鋭角である三角形を鋭角三角形（図 2）、1 つの角が直角である三角形を直角三角形（図 4）、1 つの角が鈍角である三角形を鈍角三角形（図 3）という。

また、三角形の 3 つの辺の長さに注目して、 3 つの辺の長さがすべて異なる三角形を不等辺三角形（図 2）という。

2 つの辺の長さが等しい三角形を二等辺三角形（図 5）という。

二等辺三角形のうち、直角三角形の直角をはさむ 2 つの辺が等しいものを直角二等辺三角形（図 6）という。

二等辺三角形のうち、残りの 1 つの辺の長さも含め、3 つの辺の長さがすべて等しい三角形を正三角形（図 7）という。

直角三角形

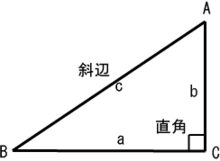
図 4: 直角三角形

直角三角形の直角の対辺を斜辺という（図 4）。斜辺は、直角三角形の 3 つの辺の中で最も長い。

斜辺を除く残りの 2 辺のことを、直角をはさむ 2 辺と呼ぶ。

直角をはさむ 2 辺 a，b と、斜辺 c の間には、次の関係が成り立つ（ピタゴラスの定理）。

a² + b² = c²

三角形で、3 辺 a，b，c の長さが、上の式を満たすとき、△ABC は辺 c を斜辺とする直角三角形である（ピタゴラスの定理の逆）。

二等辺三角形

図 5: 二等辺三角形

二等辺三角形で、長さの等しい 2 つの辺を等辺といい、残りの 1 つの辺を二等辺三角形の底辺と呼ぶ。 2 つの等辺のなす角を頂角といい、残りの 2 つの内角を底角という。頂角の対辺が底辺であり、底辺の両端の角が底角である。また、二等辺三角形で頂点と言った場合、特に底辺の対頂点を指す。

△ABC が b = c の二等辺三角形であれば、底角 ∠B = ∠C であり（二等辺三角形の底角の性質）、逆に、△ABC の 2 角が ∠B = ∠C であれば、b = c の二等辺三角形となる（二等辺三角形の成立条件）。

図 6: 直角二等辺三角形

二等辺三角形は線対称な図形であり、頂角の二等分線、底辺の垂直二等分線、頂点から底辺に引いた中線はすべて対称軸上に乗る。

二等辺三角形のうち、頂角が直角に等しいものを直角二等辺三角形という。

直角二等辺三角形の場合、直角をはさむ 2 辺が等辺にあたり、斜辺が底辺にあたる。
底角の大きさはそれぞれ 45 度となる（図 6）。

正三角形

図7: 正三角形

二等辺三角形のうち、等辺と底辺の長さが等しいものを正三角形という。（図 7）

正三角形の内角はすべて等しく 60 度となる。逆に、任意の 1 角が 60 度である二等辺三角形は正三角形である。

正三角形は、正多角形の一種である。一般の正多角形が、すべての辺が等しく、すべての内角が等しいことで定義されるが、正三角形に限って3 つの辺が等しいことのみで定義される。

正三角形には、対称軸が 3 本ある。正三角形の重心，外心，内心，垂心，フェルマー点は、すべて一致する。

面積

三角形は基本的な平面図形であり、面積の求め方も、基本的なものだけでも幾通りかが知られている。いずれの式を用いても同じ値が得られるので、その時点で明らかになっている辺の長さや頂点の角度といった要素に応じて使い分ければよい。

底辺・高さによる式

1つの辺、またはその延長線と直角に交わる直線をその辺にたてた垂線といい、垂線とその辺との交点を垂線の足または垂足という。ある辺にたてた垂線が、それに対する頂点を通るとき、垂線の足とその頂点との距離をその三角形の高さという。高さは 3 つの辺それぞれに対して定義できる。ある頂点 A の対辺 a に対する高さを h_a とするとき、面積 S は

S={frac {ah_{a}}{2}}

・・・①

で表される。

3辺による式

3辺の長さを a, b, c とし、

s={frac {a+b+c}{2}}

とするとき、面積 S は

S={sqrt {s(s-a)(s-b)(s-c)}}

・・・②

で求められる。これをヘロンの公式と呼ぶ。

また、式を変形して s を置かずに

S={frac {{sqrt {(a+b+c)(-a+b+c)(a-b+c)(a+b-c)}}}{4}}

・・・③

同じことであるが、 $A=a^{2},B=b^{2},C=c^{2}$ を用いれば、

S={frac {{sqrt {2(AB+BC+CA)-(A^{2}+B^{2}+C^{2})}}}{4}}

・・・③'

としても求められる。

2辺夾角による式

2辺の長さを a, b 、その夾角の角度を C とするとき、面積 S は

S={frac {absin C}{2}}

・・・④

で求められる。
なお、高さおよびsinの定義により、①は④で説明可能である。（①の $h_{a}$ は④の $bsin C$ に等しいため）

1辺両端角（2角夾辺）による式

1辺の長さを a 、その両端角の角度を B, C とするとき、面積 S は

S={frac {a^{2}sin Bsin C}{2sin(B+C)}}

・・・⑤

または

S={frac {a^{2}}{2(cot B+cot C)}}

・・・⑥

で求められる。

内接円・傍接円による式

内接円の半径を r 、辺 a 、辺 b 、辺 c に接する傍接円の半径をそれぞれ r_a, r_b, r_c とするとき、面積 S は

S={sqrt {rr_{a}r_{b}r_{c}}}

・・・⑦

で求められる。

直交座標による式

2次元直交座標系（直交座標平面）で、原点を含む3点 A (x_A, y_A), B (x_B, y_B), C (0, 0) を頂点とする三角形の場合、面積 S は

S={frac {|x_{A}y_{B}-x_{B}y_{A}|}{2}}

・・・⑧

で表せる。

また任意の3点 A (x_A, y_A), B (x_B, y_B), C (x_C, y_C) を頂点とする三角形の場合、面積 S は

{begin{aligned}S&={frac {|x_{A}y_{B}-x_{A}y_{C}+x_{B}y_{C}-x_{B}y_{A}+x_{C}y_{A}-x_{C}y_{B}|}{2}}\&={frac {|(x_{A}-x_{C})(y_{B}-y_{A})-(x_{A}-x_{B})(y_{C}-y_{A})|}{2}}\end{aligned}}

・・・⑨

で表せる。

極座標による式

2次元極座標系（極座標平面、円座標）で、原点を含む3点 A (r_A, θ_A), B (r_B, θ_B), C (0, 0) を頂点とする三角形の場合、面積 S は

S={frac {|r_{A}cos theta _{A}r_{B}sin theta _{B}-r_{B}cos theta _{B}r_{A}sin theta _{A}|}{2}}

・・・⑩

または

S={frac {r_{A}r_{B}sin(|theta _{A}-theta _{B}|)}{2}}

・・・⑪

で表せる。

五心

三角形は内心、外心、垂心、重心、傍心をもつ。これらをあわせて五心という。

外心を O、重心を G、垂心を H とおくと、3 点 O, G, H は一直線上にあり（この直線をオイラー線と呼ぶ）、また OG : GH = 1 : 2 である。

内心

図 8: 三角形の内心（I が内心である）

三角形の 3 つの内角の二等分線は 1 点で交わる。この点のことを内心という。内心は 3 つの辺から等距離であり、内心を中心として半径がその距離である円は 3 つの辺に接する。この円のことを内接円という。

外心

図 9: 三角形の外心（O が外心である）

三角形の3辺の垂直二等分線は1点で交わる。この点のことを外心という。外心は3つの頂点から等距離であり、外心を中心として半径がその距離である円は3つの頂点を通る。この円のことを外接円という。

外心は三角形の内部にあるとは限らない。鈍角三角形の場合は外側にあり、直角三角形の場合は斜辺の中点上にある。

垂心

図 10: 三角形の垂心（H が垂心である）

三角形の 3 つの頂点からそれぞれの対辺に引いた垂線は 1 点で交わる。この点のことを垂心という。

重心

図 11: 三角形の重心（G が重心である）

三角形の頂点とその対辺の中点を結ぶ 3 つの線分は 1 点で交わる。この点のことを重心という。また、それぞれの線分を中線といい、重心は中線を 2 : 1 の比で分割する。

傍心

図 12: 三角形の傍心（I_A, I_B, I_C がそれぞれ、傍心である）

三角形の 1 つの内角と他の 2 つの外角の二等分線は 1 点で交わる。この点のことを傍心（ぼうしん）という。三角形に傍心は 3 つある。傍心は 1 つの辺と 2 つの辺の延長線と等距離にあり、傍心を中心として半径がその距離である円を傍接円という。

三角形の 3 辺、およびその延長線上と等距離である点は、内心と傍心あわせて 4 点ある。

合同条件

2 つの三角形を移動して重ねあわせることができるとき、この 2 つの三角形は合同である。ここでいう移動とは、平行移動、回転移動、対称移動を組み合わせたものである。

ある 2 つの三角形について、以下の条件のうち 1 つでも満たしていれば、その 2 つの三角形は合同となる。これを三角形の合同条件という。この条件は「三つの条件のうち、どれかが与えられれば三角形は決定される」、「相似の特別な場合である」（これは一般の多角形についても成り立つ）と解釈する事もできる。

三辺相等: 対応する 3 辺の長さがそれぞれ等しい
二辺夾角相等（二辺挟角相等）: 対応する 2 辺の長さと、挟まれる角の大きさがそれぞれ等しい
二角夾辺相等（二角挟辺相等・一辺両端角相等）: 対応する 2 角の大きさと、挟まれる辺の長さがそれぞれ等しい

また、三角形の内角の和が 180 度である事を考えれば、必ずしも、辺を挟む 2 角が与えられていなくとも良い事が分かる。

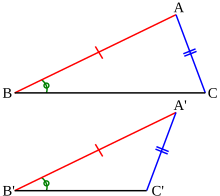
図 13: 2 辺と 1 角が等しいが合同ではない三角形の例

これに対して、2 辺と 1 角が等しい場合には、それだけでは合同であるとはいえない。例を図 13 に示す。図 13 の場合、三角形 ABC と A'B'C' について、辺 AB と A'B', AC と A'C', 角 ABC と A'B'C' が等しいが、合同ではない。

また、1 角が直角である場合、次のような合同条件も考えられる。

斜辺と他の一辺相等

斜辺と一つの鋭角相等

相似条件

ある2つの三角形について、以下の条件のうち1つでも満たしていれば、その2つの三角形は相似である。

三辺比相等（三辺の比相等）: 対応する3組の辺の長さの比が等しい
二辺比夾角相等（二辺比挟角相等・二辺の比と夾角相等・二辺の比と挟角相等）: 対応する2組の辺の長さの比と、挟まれる角の大きさがそれぞれ等しい
二角相等: 対応する2組の角の大きさがそれぞれ等しい

「三辺比相等」は、ある三角形と、また別の三角形について、対応する辺の長さがそれぞれ等しいことである。

また、ある三角形Aにおいて、辺の長さの比が、p : q : r であり、別の三角形Bにおいて、辺の長さの比も、p : q : r である場合には、三角形Aの辺の長さが ap, aq, ar とおけて、三角形Bの辺の長さが bp, bq, br とおける。すると、ap : bp = aq : bq = ar : br = a : b であり、相似といえる。

特に、正三角形（内角が全て60度）と直角二等辺三角形（内角が90,45,45度）については互いに相似である。

三角形（トライアングル）を含む語

パスカルの三角形

ハインリッヒの三角形

三角州

三角点

三角貿易

三角町

トライアングル（打楽器）

鉄のトライアングル

地域名
- 黄金の三角地帯
- バミューダ・トライアングル
- ドラゴン・トライアングル
- ポリネシアン・トライアングル
- スンニー・トライアングル

ナチ強制収容所のバッジ
- ピンク・トライアングル
- パープル・トライアングル
- ブラック・トライアングル

夏の大三角

冬の大三角

搜尋此網誌

Yrurtj

三角形

目次