スペクトル密度
スペクトル密度（スペクトルみつど、英: Spectral density）は、定常過程に関する周波数値の正実数の関数または時間に関する決定的な関数である。パワースペクトル密度（電力スペクトル密度、英: Power spectral density）、エネルギースペクトル密度（英: Energy spectral density）とも。単に信号のスペクトルと言ったとき、スペクトル密度を指すこともある。直観的には、スペクトル密度は確率過程の周波数要素を捉えるもので、周期性を識別するのを助ける。
目次
1 概要
2 定義
2.1 エネルギースペクトル密度
2.2 パワースペクトル密度
2.2.1 パワースペクトル密度の特性
3 推定
4 特性
5 関連する概念
6 応用
6.1 電子工学
6.2 測色法
7 関連項目
8 参考文献
9 外部リンク
概要
物理学の観点では、信号とは波動であり、電磁波や音波がある。波動のスペクトル密度に適当な係数をかけると、その波動で運ばれる周波数当たりの力になる。このため、それを信号の「パワースペクトル密度」(PSD) あるいは「スペクトルパワー分布」(SPD) などと呼ぶ。パワースペクトル密度の単位はヘルツ当たりのワット (W/Hz) か、ナノメートル当たりのワット (W/nm) で表される（後者は周波数の代わりに波長を用いる）。
信号がどのような物理的次元を伝わるのかは問題ではないが、以下の議論では時間と共に変化する信号について解説する。
定義
エネルギースペクトル密度
エネルギースペクトル密度 (ESD) は、信号や時系列のエネルギーが周波数についてどのように分布するかを示す。f(t) が有限エネルギー信号であるとき、その信号のスペクトル密度 ESD(ω) は、信号をフーリエ変換したときの大きさの2乗である（ここで、エネルギーは信号の2乗を積分したものであり、その信号を電圧として 1Ω の負荷に加えたときの物理エネルギーに等しい）。
ESD(ω)=|12π∫−∞∞f(t)e−iωtdt|2=F(ω)F∗(ω)2π{displaystyle ESD(omega )=left|{frac {1}{sqrt {2pi }}}int _{-infty }^{infty }f(t)e^{-iomega t},dtright|^{2}={frac {F(omega )F^{*}(omega )}{2pi }}}
ここで ω は角周波数（周波数に 2π{displaystyle 2pi } を掛けたもの）であり、F(ω) は f(t) の連続フーリエ変換、F*(ω) はその複素共役である。12π{displaystyle {frac {1}{2}}pi } という係数は絶対的なものではなく、フーリエ変換での正規化定数の定義に依存する。
例として、f(t) が伝送路を通って伝播する電気信号の電位を（ボルトで）表す場合、スペクトル密度 ESD(ω) の測定単位は volt2×seconds2 として現れるが、物理学のスペクトルのエネルギー密度としてはまだ次元的に正確ではない。しかしながら、（オームで表される）伝送路の特性インピーダンス Z によって除算すると、ESD(ω) の次元は1オーム当たり volt2×seconds2 になる。これは、1 ヘルツ当たりのジュール（物理学で定義されるスペクトルのエネルギー密度の国際単位）と等価となる。
信号が離散的で、値が fn = f(n,dt) で表されるとした場合、無限に続くとするならエネルギースペクトル密度は次のように得られる。
ESD(ω)=|dt2π∑n=−∞∞fne−iωn|2=dt22πFd(ω)Fd∗(ω){displaystyle ESD(omega )=left|{frac {dt}{sqrt {2pi }}}sum _{n=-infty }^{infty }f_{n}e^{-iomega n}right|^{2}={frac {dt^{2}}{2pi }}F_{d}(omega )F_{d}^{*}(omega )}
ここで、F(ω) は fn の離散時間フーリエ変換である。数学ではサンプリング間隔 dt を 1 として扱うことが多い。しかしながら、正確な物理単位を維持するためと、dt → 0 とした場合に連続時間の関数へ逆変換できることを保証するためには dt が必要となる。
パワースペクトル密度
上述のエネルギースペクトル密度の定義は、信号のフーリエ変換が存在するパルスのような信号に最も適している。たとえば定常物理過程を示す連続信号について、パワースペクトル密度あるいは電力スペクトル密度 (PSD) を定義することは価値があり、信号や時系列の力が周波数についてどのように分布しているかを示す。ここでいう力とは具体的な物理的力であり、抽象的な信号についても、信号の2乗と定義できる。このとき、信号 f(t) のある一瞬の力は次のように与えられる。
P(t) = f(t)2
平均（あるいは期待値）としての P(t) は力の合計であり、全周波数領域にわたる電力スペクトル密度の積分である。
正規化されたフーリエ変換:
- FT(ω)=1T∫0Tf(t)exp(−iωt),dt{displaystyle {mathcal {F}}_{T}(omega )={frac {1}{sqrt {T}}}int _{0}^{T}f(t)exp(-iomega t),dt}
を使用して、次のようにパワースペクトル密度を定義できる[1][2]。
- PSD(ω)=limT→∞E[|FT(ω)|2]{displaystyle PSD(omega )=lim _{Trightarrow infty }mathbf {E} left[|{mathcal {F}}_{T}(omega )|^{2}right]}
![{displaystyle PSD(omega )=lim _{Trightarrow infty }mathbf {E} left[|{mathcal {F}}_{T}(omega )|^{2}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dde9883d60fe5cfd45e9cf177bb57296c0e03bd2)
確率論的な信号については、フーリエ変換の二乗値は一般的に極限に近づけないが、期待は行う。（ピリオドグラムを参照。）
見解：取り扱う多くの信号が積分可能ではなく、その信号の 非正規化（＝通常の） フーリエ変換は存在しない。何人かの著者（たとえば Risken[3]）は、まだ非正規化フーリエ変換を使ってパワースペクトル密度の定義
- ⟨F(ω)F∗(ω′)⟩=2πPSD(ω)δ(ω−ω′){displaystyle langle F(omega )F^{ast }(omega ')rangle =2pi ,PSD(omega ),delta (omega -omega ')}
を公式化している。ここで、δ(ω − ω') はディラックのデルタ関数である。このような公式の文献は直観を導くには有用であるが、十分な注意と共に使用されるべきである。
このような形式推論を用いると、定常ランダム過程とパワースペクトル密度 PSD(ω) およびこの信号の自己相関関数 R(τ) = <f(t) f(t + τ)> がフーリエ変換対でなければならないことに気づくだろう。このことは真実であり、ノーバート・ウィーナーおよびアレクサンドル・ヒンチンによって作り出された意味深い定理（ウィーナー・ヒンチンの定理）となる。
- PSD(f)=∫−∞∞R(τ)e−iωτdτ=F(R(τ)){displaystyle PSD(f)=int _{-infty }^{infty },R(tau ),e^{-iomega tau },dtau ={mathcal {F}}(R(tau ))}
多くの著者が、実際にパワースペクトル密度を 定義する ためにこの等式を使用している[4]。そうする理由は「数学的曖昧さ」を回避するためであると、多くの書籍に記載されている。
ある周波数帯域 [ω1, ω2] における信号の力は、正の周波数と負の周波数について積分することで計算できる。
- P=∫ω1ω2PSD(ω)+PSD(−ω)dω{displaystyle P=int _{omega _{1}}^{omega _{2}},PSD(omega )+PSD(-omega ),domega }
信号のパワースペクトル密度は、その信号が広義の定常過程であるときだけ存在する。信号が広義、もしくは、狭義の定常過程でない場合、その自己相関関数は2つの変数の関数となる。広義の 周期定常過程 のような場合、PSD は存在する可能性がある[5]。
より一般に、似たような技法で時と共に変化するスペクトル密度の近似を求めることができる。
パワースペクトル密度の定義は、全測定時間 T =n dt の間に離散時間 fn = f(n,dt) でサンプリングされた信号のような有限の時系列 fn = f(n,dt)（ただし 1 ≤ n ≤ N）を直接的に一般化する。
PSD(ω)=dt2T|∑n=1Nfne−iωn|2{displaystyle PSD(omega )={frac {dt^{2}}{T}}left|sum _{n=1}^{N}f_{n}e^{-iomega n}right|^{2}}.
実世界の応用では、観察された物理過程の基礎となる実際の PSD のより正確な推定を行うために、一度の測定で得られる PSD の結果を複数回反復測定し平均化することが一般的である。このように計算された PSD はピリオドグラムと呼ばれる。平均する時間間隔Tを無限に近づける場合、ピリオドグラムが真のパワースペクトル密度 (PSD) に近づくことを証明できる（ブラウンとホワン[6]）。
2つの信号共に パワースペクトラ （正確な用語；spectrum の複数形は spectra）を有する場合、これらの相互相関関数を用いてクロスパワースペクトルを計算できる。
パワースペクトル密度の特性
PSD には次のような特性がある[7]。
- 実際に使われる過程のスペクトルは対称である: S(− f) = S(f) 言い換えると、偶関数である。
- [− 1/2, +1/2] の範囲で連続しており、微分可能である。
- PSD の微分は f = 0 で 0 となる。（このことはパワースペクトルが偶関数となるために必要である。）そうでない場合、微分は f = 0 で存在しない可能性がある。
自己共分散関数はフーリエ逆変換を使うことにより再構成することができる。- PSD は、時間軸上の分散の分布を示している。とりわけ、
Var(Xt)=γ0=2∫01/2S(ω)dω{displaystyle {text{Var}}(X_{t})=gamma _{0}=2int _{0}^{1/2}S(omega )domega } である。
- PSD は自己共分散関数の一次関数となる。
- もし γ が2つの関数 γ(τ) = α1γ1(τ) + α1γ2(τ) に再構成される場合、
S(f) = α1S1(f) + α2S2(f) となる。
- ここで Si(f)=F{γi}{displaystyle S_{i}(f)={mathcal {F}}{gamma _{i}}}
- ここで Si(f)=F{γi}{displaystyle S_{i}(f)={mathcal {F}}{gamma _{i}}}
パワースペクトル G(f) は次式で定義される[8]。
- G(f)=∫−∞fS(f′)df′.{displaystyle G(f)=int _{-infty }^{f}S(f^{prime }),df^{prime }.}
推定
スペクトル密度推定の目的は、連続した時間サンプルからランダム信号のスペクトル密度を推定（estimate）することである。
信号から何が知られているかに依存するが、推定方法は パラメトリック推定 と非パラメトリック推定の2つの方法があり、時間領域または周波数領域の分析が基本となる。たとえば、パラメトリック推定 で共通の技術は自己回帰モデルに観測を適応させることを含んでいる。非パラメトリック推定で共通の技術はピリオドグラムである。
スペクトル密度は通常フーリエ変換法を使用して推定されるが、ウェルチ法や最大エントロピー法といった他の技術も使用することができる。
特性
f(t) のスペクトル密度と f(t) の自己相関は、フーリエ変換対を形成する（PSD と ESD とで、自己相関関数の異なる定義が使われる）。- フーリエ解析の1つの結果としてパーセバルの定理がある。それによると、エネルギースペクトル密度の曲線の面積は、信号の振幅の自乗すなわち全エネルギーの面積に等しい。
∫−∞∞|f(t)|2dt=∫−∞∞Φ(ω)dω.{displaystyle int _{-infty }^{infty }left|f(t)right|^{2},dt=int _{-infty }^{infty }Phi (omega ),domega .}
この定理は離散的な場合でも成り立つ。同様にパワースペクトル密度の積分したものは、それに対応する信号の全エネルギーの平均に等しい（それはまた、遅延ゼロでの自己相関関数である）。
関連する概念
- 周波数分布を示すグラフは、ほとんどの場合スペクトル密度を表している。完全な周波数スペクトルを描く場合、振幅と周波数のグラフ（スペクトル密度に相当）と位相と周波数のグラフ（スペクトル密度以外の情報）で表される。信号 f(t) の波形は、完全な周波数スペクトルがあれば再現できる。信号 f(t) をスペクトル密度情報だけから再現することはできない。
- スペクトル密度関数の中点を、その信号のスペクトル重心と呼ぶ。すなわち、その周波数を分割点として、上と下でエネルギーが拮抗する。
- スペクトル密度は周波数の関数であって、時間の関数ではない。しかし、長い信号の非常に短い期間のスペクトル密度を計算することもでき、それらを時系列に並べることもできる。そのようなグラフをスペクトログラムと呼ぶ。これは、短時間フーリエ変換やウェーブレット変換などのスペクトル解析技法の基本である。
応用
電子工学
信号のパワースペクトル密度は電子工学の基本概念の1つであり、特に電子通信システム（無線、レーダーなど）で重要である。電気信号のパワースペクトルを測定して表示する機器としてスペクトラムアナライザがある。
スペクトラムアナライザは、入力信号の短時間フーリエ変換 (STFT) の絶対値を測るのが基本である。解析対象の信号が定常的ならば、STFT はパワースペクトル密度のよい近似となる。
測色法
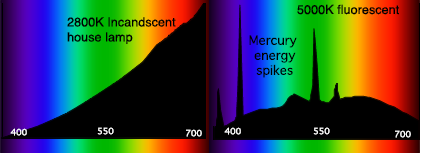
光のスペクトルとは、色に対応した各周波数で運ばれる力を示したものである。光スペクトルは周波数よりも波長で表されることが多く、厳密にはスペクトル密度ではない。分光測色器によっては、1から2ナノメートル単位の分解能を持つ。値は他の用途に使われたり、光源のスペクトル属性を示すために図示されたりする。これを使って光源の色特性を解析する。
関連項目
- ノイズスペクトル密度
- ノイズ
- スペクトル漏れ
- 窓関数
- 周波数領域
- 周波数スペクトル
- バイスペクトル
- スペクトル解析
- スペクトログラム
- スペクトラムアナライザ
参考文献
^ Fred Rieke, William Bialek, and David Warland (1999). Spikes: Exploring the Neural Code (Computational Neuroscience). MIT Press. ISBN 978-0262681087.
^ Scott Millers and Donald Childers (2012). Probability and random processes. Academic Press.
^
Hannes Risken (1996). The Fokker–Planck Equation: Methods of Solution and Applications (2nd ed.). Springer. p. 30. ISBN 9783540615309. http://books.google.com/books?id=MG2V9vTgSgEC&pg=PA30.
^ Dennis Ward Ricker (2003). Echo Signal Processing. Springer. ISBN 1-4020-7395-X. http://books.google.com/books?id=NF2Tmty9nugC&pg=PA23&dq=%22power+spectral+density%22+%22energy+spectral+density%22&lr=&as_brr=3&ei=HZMvSPSWFZyStwPWsfyBAw&sig=1ZZcHwxXkErvNXtAHv21ijTXoP8#PPA23,M1.
^
Andreas F. Molisch (2011). Wireless Communications (2nd ed.). John Wiley and Sons. p. 194. ISBN 978-0-470-74187-0. http://books.google.com/books?id=vASyH5-jfMYC&pg=PA194.
^ Robert Grover Brown & Patrick Y.C. Hwang (1997). Introduction to Random Signals and Applied Kalman Filtering. John Wiley & Sons. ISBN 0-471-12839-2. http://www.amazon.com/dp/0471128392.
^ Storch, H. Von; F. W Zwiers (2001). Statistical analysis in climate research. Cambridge Univ Pr. ISBN 0-521-01230-9.
^ An Introduction to the Theory of Random Signals and Noise, Wilbur B. Davenport and Willian L. Root, IEEE Press, New York, 1987, ISBN 0-87942-235-1
外部リンク
時系列データ解析におけるパワースペクトル密度関数について Cygnus Research International- スペクトル解析の基礎知識
