Yrurtj

この項目では、本来の数学用語の偏差値について説明しています。学校受験で用いられる、学力を測る数値については「学力偏差値」をご覧ください。

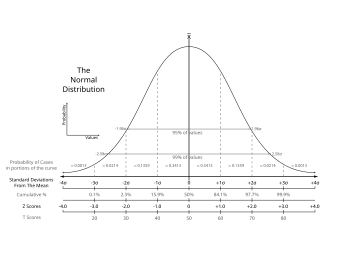
正規分布曲線と偏差値の関係。T scoresが偏差値を示す。

偏差値（へんさち、英: standard score）とは、ある数値がサンプルの中でどれくらいの位置にいるかを表した無次元数。平均値が50、標準偏差が10となるように標本変数を規格化したものである。

概要

偏差値の利用価値が高いのは、サンプルの数値の分布が正規分布に近い状態の時である。分布のピークが2箇所ある場合など、正規分布と大きく異なる場合には適切な指標となりえない場合がある。

標本が正規分布する場合は、40から60の間に約68.3%、30から70の間に約95.4%、20から80の間に約99.73%、10から90の間に約99.9937%、0から100の間に約99.999953%が含まれる事が知られている^[1]。つまり、

• 偏差値60以上（あるいは40以下）は、全体の15.866％。


• 偏差値70以上（あるいは30以下）は、全体の2.275％。


• 偏差値80以上（あるいは20以下）は、全体の0.13499％。


• 偏差値90以上（あるいは10以下）は、全体の0.00315％。


• 偏差値100以上（あるいは0以下）は、全体の0.00002％。

例えば、全受験生が100万人いた学力試験で偏差値を求めると、偏差値80以上となる者は、ほぼ1350人となる。(日本の実際の統計では、10代における同じ年齢の人口はおおよそ110〜120万人程度。40代は180〜200万人程度)

平均値から大きく離れた場合は0から100の間に収まらないが、その割合は非常に低く、約0.000047%、つまり約200万分の1しかない。偏差値の上限値、下限値は元となる標本の分布によって決まるものであり、いかなる実数をもとりうる。

数式による解説

偏差値T_i は次の式で求まる。

Ti=10(xi−μx)σx+50{displaystyle T_{i}={frac {10(x_{i}-mu _{x})}{sigma _{x}}}+50}

ただし、

μx=1N∑i=1Nxiσx=1N∑i=1N(xi−μx)2=1N∑i=1Nxi2−μx2{displaystyle {begin{aligned}&mu _{x}={frac {1}{N}}sum _{i=1}^{N}x_{i}\&sigma _{x}={sqrt {{frac {1}{N}}{sum _{i=1}^{N}(x_{i}-mu _{x})^{2}}}}={sqrt {{frac {1}{N}}{sum _{i=1}^{N}x_{i}^{2}-mu _{x}^{2}}}}\end{aligned}}}

N ：サンプルの大きさ　x_i ：個々の値（標本値）　μ_x ：算術平均　σ_x ：標準偏差

である。なお分母σ_x は標準偏差であり、分子x_i - μ_x は偏差である。偏差が 0 であるとき（ある標本値x_i が平均値μ_x に等しいとき）は偏差値は 50 となる。また、全ての標本値x_i が同じ値であるときは標準偏差σ_x = 0 となってしまうためこの式では偏差値は定義できないが、その場合は便宜上全ての標本値の偏差値を 50 と考えることがある。

応用例

この節には独自研究が含まれているおそれがあります。問題箇所を検証し出典を追加して、記事の改善にご協力ください。議論はノートを参照してください。（2009年5月）

• 
  学力検査の結果を表す学力偏差値は、入学試験の合格率の判定などに広く使われている。


• 
  知能検査の結果を表す知能偏差値は、教育などに役立てるために、知能指数などとともに使われている。


• 何らかの格付け表が作成される場合、比喩的に偏差値が用いられる事がしばしばある。

脚注

関連項目

• 統計


• 標準得点


• 
  標準偏差 - 正規分布
  


• 学力偏差値


• 顔面偏差値